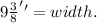Question

The perimeter of a rectangle is 38”. If the length is 3” morb than the width, find the width

Answer 1

To answer this question we will use the following formula for the perimeter of a rectangle:

`Perimeter=2(length+width).`

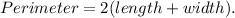
Since the perimeter of the rectangle is 38'' and the length is 3''' more than the width, then we can set the following system of equations:

Substituting the second equation in the first one we get:

`38^(\prime\prime)=2(width+3^(\prime)^(\prime)^(\prime)+width).`

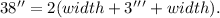
Simplifying the above result we get:

`\begin{gathered} 38^(\prime)^(\prime)=2(2width+3^(\prime)^(\prime)^(\prime)) \\ =4width+6^(\prime\prime\prime). \end{gathered}`

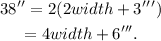
We know that:

`1^(\prime)^(\prime)^(\prime)=(1)/(12)^(\prime)^(\prime).`

Therefore:

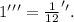
`38^(\prime)^(\prime)^=4width+(1)/(2)^(\prime)^(\prime).`

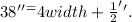
Subtracting 1/2'' from the above result we get:

`\begin{gathered} 38^(\prime)^(\prime)-(1)/(2)^(\prime)^(\prime)=4width+(1)/(2)^(\prime)^(\prime)-(1)/(2)^(\prime)^(\prime), \\ 37(1)/(2)^(\prime)^(\prime)=4width. \end{gathered}`

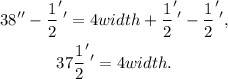
Dividing the above result by 4 we get:

`9(3)/(8)^(\prime)^(\prime)=width.`