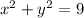Question

The foci of the hyperbola lie on the circle. Write an equation of the circle. Show all work.The equation of the hyperbola: \small \frac{x^2}{4}-\frac{y^2}{5}=1

Answer 1

Given the equation of the hyperbola:

`(x^2)/(4)-(y^2)/(5)=1`

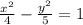
The general equation of the hyperbola:

`(x^2)/(a^2)-(y^2)/(b^2)=1`

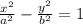
Comparing the given equation with general form:

`\begin{gathered} a^2=4,b^2=5 \\ c^2=a^2+b^2=4+5=9 \\ c=\pm\sqrt[]{9}=\pm3 \end{gathered}`

So, the coordinates of the foci are:

`(-3,0),(3,0)`

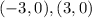
Now, we will find the equation of the circle that has a diameter with the endpoints (-3, 0) and (3,0)

The center of the circle = (0,0)

and the radius of the circle = r = 3

the general equation of the circle with the center (0,0) is as follows:

`x^2+y^2=r^2`

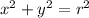
So, the answer will be the equation of the circle will be:

`x^2+y^2=9`