First, to determinate which numbers can be written as a rational or irrational, first we need to define those two terms.
A rational number is any real number that can be expressed as the quotient of two integers.
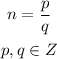
n is a rational number.
A irrational number is any real number that cannot be expressed as the quotient of two integers.
Now that we know what a rational number is, let's check the items in the question.
For the item A, we have:
![(5)/(6)+\frac{\sqrt[]{12}}{3}](https://img.qammunity.org/2023/formulas/mathematics/college/oxnmwvmqswcw6oxc8uh2lj9f4lx7n4r4yc.png)
To simplify this expression, first let's multiply both numerator and denominator of the second term by 2, so we can make the denominators of both terms equal.
![(5)/(6)+\frac{\sqrt[]{12}}{3}=(5)/(6)+\frac{2*\sqrt[]{12}}{2*3}=(5)/(6)+\frac{2\sqrt[]{12}}{6}=\frac{5+2\sqrt[]{12}}{6}](https://img.qammunity.org/2023/formulas/mathematics/college/ksab6zx3ibur10r590kqbb5fwqf82hshqx.png)
We can also simplify the square root of twelve
![\frac{5+2\sqrt[]{12}}{6}=\frac{5+2\sqrt[]{3*4}}{6}=\frac{5+2\sqrt[]{3}\sqrt[]{4}}{6}=\frac{5+4\sqrt[]{3}}{6}](https://img.qammunity.org/2023/formulas/mathematics/college/tgs53fddlod32jc5qaqe6tngk5khmb0rlf.png)
This is the simplest form of writing the number as a single fraction. Now, let's analyze the numerator and denominator.
![6\in Z,(5+4\sqrt[]{3})\\otin Z](https://img.qammunity.org/2023/formulas/mathematics/college/ba5bvxvl56b5iwuqqonzfgx8j4ziwkhrxw.png)
Since the numerator isn't an integer, then this number is not rational.
Now, let's check the number for item B.
Our number is
![(5)/(6)-\frac{\sqrt[]{36}}{3}](https://img.qammunity.org/2023/formulas/mathematics/college/l02vgk6pynxej5shp0iyus19kfsadgxqpy.png)
Again, let's make the denominators equal:
![(5)/(6)-\frac{\sqrt[]{36}}{3}=(5)/(6)-\frac{2*\sqrt[]{36}}{2*3}=(5)/(6)-\frac{2\sqrt[]{36}}{6}=\frac{5-2\sqrt[]{36}}{6}](https://img.qammunity.org/2023/formulas/mathematics/college/u6np2qhl04awoi2a67z5pk95odxz1v8det.png)
36 is a perfect square, and its square root is 6.
![\frac{5-2\sqrt[]{36}}{6}=(5-2*6)/(6)=(5-12)/(6)=(-7)/(6)](https://img.qammunity.org/2023/formulas/mathematics/college/1z86k5szk1gr4snheg7mycsvr83pkmp1mb.png)
Since - 7 and 6 are both integers, this number is rational.
The number for item C:
![(5)/(6)\frac{\sqrt[]{12}}{3}](https://img.qammunity.org/2023/formulas/mathematics/college/tlz59nmucjusa0kzpqumwddi01w3uxuptl.png)
When we want to do a product between two fractions, we just multiply denominator by denominator, and numerator by numerator:
![(5)/(6)\frac{\sqrt[]{12}}{3}=\frac{5*\sqrt[]{12}}{6*3}=\frac{5\sqrt[]{12}}{18}](https://img.qammunity.org/2023/formulas/mathematics/college/o6u9p9yiygg3ctd575957p1tx9vvixuhsg.png)
We can simplify this expression the same way we did on item A.
![\frac{5\sqrt[]{12}}{18}=\frac{10\sqrt[]{3}}{18}=\frac{5\sqrt[]{3}}{9}](https://img.qammunity.org/2023/formulas/mathematics/college/ehug5or8fey3yqcpmwf34l1vx7ruffg47r.png)
Since the numerator is not an integer
![5\sqrt[]{3}\\otin Z](https://img.qammunity.org/2023/formulas/mathematics/college/10vd7mly2r4fvyb2baez7x4b99qg3p2w5v.png)
This number is not rational.
For the last item, D, we have:
![(5)/(6)\colon\frac{\sqrt[]{36}}{3}](https://img.qammunity.org/2023/formulas/mathematics/college/l7shbgnw5vh66hvk954jisussc5o9fwww5.png)
Dividing a fraction by other, is the same as multiplying the first one by the inverse of the other.
![(5)/(6)\colon\frac{\sqrt[]{36}}{3}=(5)/(6)*\frac{3}{\sqrt[]{36}}=\frac{15}{6\sqrt[]{36}}=(15)/(36)=(5)/(12)](https://img.qammunity.org/2023/formulas/mathematics/college/tu1p6g6jybgr2j2b13b818csa4mdzgpg7u.png)
Since both 5 and 12 are integers, this number is rational.