Question

All 5-digit zip codes in the United States are assigned by region. In one particularstate, all zip codes begin with the number 3 while the second digit is restricted tonumbers from 3 to 7. There is no restriction on the remaining digits. How manyzip code combinations are possible in this particular state? (8 points)

Answer 1

We want to determine the number of zip code combinations possible for the state.

Given that;

- all zip codes begin with the number 3

- the second digit is restricted to numbers from 3 to 7

- the remaining digits have no restriction.

With the above conditions;

the first digit can only be one number which is 3, so;

`N_1=1`

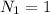
the second digit can be just 2 numbers either 3 or 7, so;

`N_2=2`

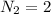
The remaining digits have 10 possible numbers each from 0 to 9, so;

`N_3=N_4=N_5=10`

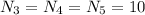
substituting this values into the formula given, we have;

`\begin{gathered} N=N_1* N_2* N_3* N_4* N_5 \\ N=1*2*10*10*10 \\ N=2000 \end{gathered}`

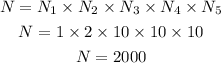
Therefore, the state have 2000 possible zip code combinations.