Given
The perimeter of the reactangle is, P = 48 inches
The objective is to find the difference between the greatest and least areas that the rectangle.
The sum of the length and breadth of the reactangle can be calculated using the formula of perimeter of the rectangle.
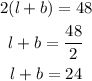
The various possible pairs for obtaining 24 are,

From the above pairs, consider the first and the last pairs.
The least area of the rectangle will be,
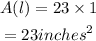
The greatest area of the rectangle will be,

Then, the difference can be calculated as,
![undefined]()