Question

On Monday Harold picked up six donuts and two large coffees for the office staff. He paid $5.80. On Tuesday, Melinda picked up four donuts and 5 large coffees for the office staff. She paid $7.02. What is the cost of one donut? What is the cost of one large coffee?

Answer 1

Cost of tjhe donut: D

Cost of the large coffee: C

On Monday Harold picked up six donuts and two large coffees for the office staff, he paid $5.80:

`6D+2C=5.80`

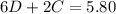
On Tuesday, Melinda picked up four donuts and 5 large coffees for the office staff. She paid $7.02:

`4D+5C=7.02`

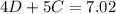
Use the next system of linear equations to find the value of D and C:

`\begin{gathered} 6D+2C=5.80 \\ 4D+5C=7.02 \end{gathered}`

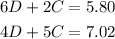
1. Solve D in the first equation:

`\begin{gathered} \text{Subtract 2C in both sides of the equation:} \\ 6D+2C-2C=5.80-2C \\ 6D=5.80-2C \\ \\ \text{Divide both sides of the equation into 6:} \\ (6)/(6)D=(5.80)/(6)-(2)/(6)C \\ \\ D=(5.80)/(6)-(1)/(3)C \end{gathered}`

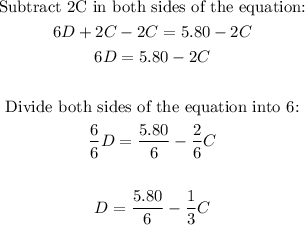
2. Substitute the D in the second equation by the equation you get in step 1:

`4((5.80)/(6)-(1)/(3)C)+5C=7.02`

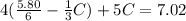
3. Solve C:

`\begin{gathered} (23.2)/(6)-(4)/(3)C+5C=7.02 \\ \\ (-4C+15C)/(3)=7.02-(23.2)/(6) \\ \\ (11)/(3)C=(42.12-23.2)/(6) \\ \\ (11)/(3)C=(18.92)/(6) \\ \\ C=(3)/(11)\cdot(18.92)/(6) \\ \\ C=(56.76)/(66) \\ \\ C=0.86 \end{gathered}`

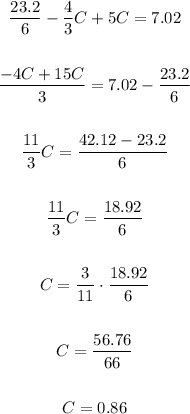
4. Use the value of C=0.86 to find D;

`\begin{gathered} D=(5.80)/(6)-(1)/(3)C \\ \\ D=(5.80)/(6)-(1)/(3)(0.86) \\ \\ D=(5.80)/(6)-(0.86)/(3) \\ \\ D=(17.4-5.16)/(18) \\ \\ D=(12.24)/(18) \\ \\ D=0.68 \end{gathered}`

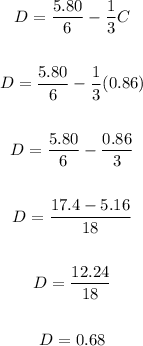
The solution fot the system is:

`\begin{gathered} C=0.86 \\ D=0.68 \end{gathered}`

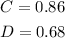
The cost of one dount is $0.68

The cost of one large coffee is $0.86