We can use the distance formula to find the distance between A and B.
Given,
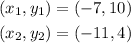
The distance formula is
![D=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/bn18956xdzpj56va064oiuu2531qoyd8xa.png)
Substituting in the respective points and simplifying, we can find the distance:
![\begin{gathered} D=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2} \\ D=\sqrt[]{(4-10_{})^2+(-11-(-7))^2} \\ D=\sqrt[]{(-6)^2+(-4)^2} \\ D=\sqrt[]{36+16} \\ D=\sqrt[]{52} \\ D=\sqrt[]{4\cdot13} \\ D=\sqrt[]{4}\sqrt[]{13} \\ D=2\sqrt[]{13} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/2o78swf6hfinf3lg5d8kul1lg7chgd6qne.png)
**Note
The radical property used to simplify the last steps are:
![\sqrt[]{ab}=\sqrt[]{a}\sqrt[]{b}](https://img.qammunity.org/2023/formulas/mathematics/college/36x8mrtqxls717blnt9mq87duprn6qlre4.png)
Answer
![2\sqrt[]{13}](https://img.qammunity.org/2023/formulas/mathematics/college/aox4s2cqq2pot62dwmz3ejgy7cqahdieac.png)