Question

A camera has a lens diameter of 0.0444m. What wavelength of light INNANOMETERS must it use to resolvetwo objects 550 m away that are0.00718 m apart?[?] nm

Answer 1

Given:

• Diameter, D = 0.0444 m

,

• Distance, x = 0.00718 m

,

• d = 550 m

Let's find the wavelength in nanometers.

Apply the formula:

`sin\theta=(1.22\lambda)/(D)`

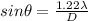
Where:

λ is the wavelength,

Also, we have the formula:

`\begin{gathered} sin\theta=(x)/(d) \\ \\ sin\theta=(0.00718)/(550) \\ \\ sin\theta=1.30545*10^(-5)\text{ m} \end{gathered}`

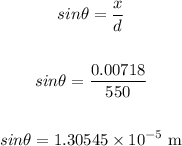
Now, plug in 1.30545 x 10⁻⁵ m for sinθ in the first equation.

Where:

D = 0.0444

Thus, we have:

`\begin{gathered} sin\theta=(1.22\lambda)/(D) \\ \\ 1.30545*10^(-5)=(1.22\lambda)/(0.0444) \\ \\ \lambda=(1.30545*10^(-5)*0.0444)/(1.22) \\ \\ \lambda=(5.796*10^(-7))/(1.22) \\ \\ \lambda=4.751*10^(-7)m \end{gathered}`

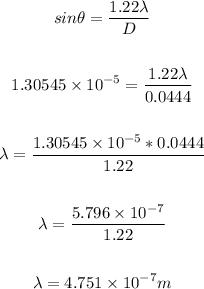
In nanometers, the wavelength will be:

`\begin{gathered} \lambda=475.1*10^(-9)m \\ \\ \lambda=475.1\text{ nm} \end{gathered}`

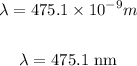
Therefore, the wavelength in nanometers is 475.1 nm.

• ANSWER:

475.1 nm