8
Step-by-step explanationto solve this we can start from the pattern function and check the transformation(s) made,so
Step 1
a) given the patter function
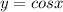
we know that the maximum values of the function cos x are:
Maximum value of sin A is 1 when A = 90 degrees
som the maximum value for the pattern function cos x is 1
Step 2
now, let's check the transformation
we have the function
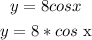
so, the pattern function was multiplied by 8, when you multiply f(x) by a constant, a, the graph of f(x) is stretched vertically. The x-intercepts remain fixed because the y-value of these points is 0, which doesn't change when you multiply it by a constant,Multiplying the sine or cosine function by a constant (positive or negative) changes the maximum height and depth of its graph. so
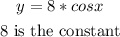
so, the maximum will be 8 times the maximum of the patter function
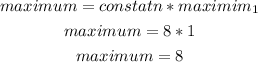
therefore, the answer is
8I hope this helps you