Question

Use the second derivative test to classify the relative extrema of the following function

Answer 1

So, here we have the function:

`f(x)=-x^2-4x+5`

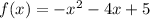
We want to check if there's a relative maxima or minima using the second deritative test.

So, let's find the first deritative of f(x). That is:

`f^(\prime)(x)=-2x-4`

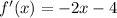
And, the second deritative can be found if we differenciate the first deritative:

`f^(\doubleprime)(x)=-2`

The second deritative test tells us that:

If f(x) has a critical point for which f'(x)=0, and the second deritative is negative at this point, then f has a local maximum.

So, as you can see, f''(x) = -2, so the second deritative will always be negative. That means, that there's a relative maxima.

Now, let's find the critical point:

`f^(\prime)(x)=0\to-2x-4=0\to-2x=4\to x=-2`

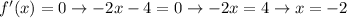
The critical point is located at x=-2. So, if we replace x=-2 in the function, we'll obtain the y-coordinate of this relative maximum.

`\begin{gathered} f(-2)=-(-2)^2-4(-2)+5 \\ f(-2)=-4+8+5 \\ f(-2)=9 \end{gathered}`

Therefore, there's a relative maxima at the point (-2,9)