Question

Does the table below show a proportional relationship? If so, what is the value of y when x is 10? If not, explain why not.

Answer 1

• Yes, the table shows a proportional relationship.

,

• When x=10, y=5

Explanation:

If y is proportionally related to x, then the equation of proportionality is given as:

`\begin{gathered} y=kx \\ k=\text{ the constant of proportion} \end{gathered}`

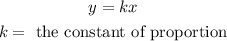
From the table:

When x=5, y=2.5

`\begin{gathered} 2.5=5k \\ k=(2.5)/(5) \\ k=0.5 \end{gathered}`

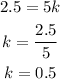
When x=8, y=4

`\begin{gathered} 4=8k \\ k=(4)/(8) \\ k=0.5 \end{gathered}`

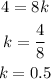
Since the values of k in both cases are the same, the table shows a proportional relationship.

When x=10

`\begin{gathered} y=kx \\ y=0.5*10 \\ y=5 \end{gathered}`

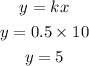
The value of y when x=10 is 5.