The linear model is:
y= - 0.06x + 26
The question says:
1. It will take William 26 litres to fill up his fish tank
2. It will take William 20.9 litres to fill up his tank if he puts 85 marbles in the fish tank.
Therefore, we now have two scenarios:
1 with 85 marbles and 20.9 litres of water and 1 without any marble and 26 litres of water.
Notice that when the number of marbles was zero, the litres of water required to fill up the fish tank was 26 while when the marbles increased to 85, the litres of water the fish tank could hold became 20.9.
This means that as the number of marbles in the fish tank increases, the amount of water it can hold reduces. This leads to a negative rate relationship between the amount of water and the number of marbles
Therefore, this situation is good enough to create a linear model of the form:
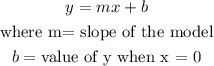
If we take the number of marbles in the fish tank as x
And we take the litres of water in the fish tank as y
In order to find the slope (m) of the linear model, we must use the formula:
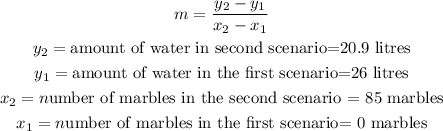
Thus, we can calculate the slope (m) as:
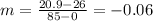
The slope (m) is negative because there is "a negative rate relationship between the amount of water and number of marbles" as stated earlier.
We have already stated that y-intercept (b) is the value when number of marbles in the fish
tank is zero.
Therefore,
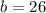
Thus, we can now write the linear model as:
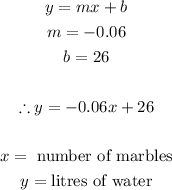
The linear model is:
y= - 0.06x + 26