Question

Hello, need help.I think the answer is D, but i am not sure.

Answer 1

GIVEN

The mean of the distribution is 75% with a standard deviation of 8%. Edna scores 85% on the test.

SOLUTION

The z-score can be used to get the percentage that Edna's score falls into. The formula is given to be:

`z=\frac{x-\overline{x}}{\sigma}`

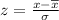
From the information provided, the following parameters can be substituted into the formula:

`\begin{gathered} x=85 \\ \overline{x}=75 \\ \sigma=8 \\ \therefore \\ z=(85-75)/(8)=(10)/(8)=1.25 \end{gathered}`

Using tables, the score corresponds to 89.44% of her class.

Therefore, Edna doesn't rank in the top 10% of her class because approximately 10.6% of the class scored bove her.

OPTION D is the correct option.