Question

Francine McFly is a 50kg circus acrobat. She does a famous stunt where she stands 2m fromthe middle of a seesaw while two of her friends jump 2m from the middle of the other sideof the seesaw. A third stomps the seesaw. The two jumpers each weigh 80Kg and reach a max height of 1m. The stomper stomps with an energy equivalent to ¼ of one of the jumpers. Francine then does a backflip onto the shoulders of 3 of her friends. a) Francine's Velocity when she is shot off andb) How HIGH Francine gets.

Answer 1

Given,

The mass of Francine McFly, m=50 kg

The distance from the center of the seesaw to Francine, d=2 m

The mass of the jumpers, M=80 kg

The maximum height reached by the jumpers, h=1 m

From the law of conservation of energy, energy can neither be created nor be destroyed but can be converted from one form to another.

The jumpers transfer their potential energy to Francine through the seesaw. The energy gained by Francine from jumpers and a stomper gives her the velocity. She shots off with the kinetic energy equal to the total energy transferred input of two jumpers and a stomper. As Francine rises, she slowly loses kinetic energy. This lost kinetic energy will be converted into her potential energy. When she reaches the top, her potential energy will be equal to the energy input from the two jumpers and a stomper.

The energy applied by two jumpers is equal to their potential energy at the maximum height, That is,

`\begin{gathered} E=M\text{gh}+M\text{gh} \\ =2M\text{gh} \end{gathered}`

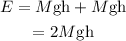
Where g is the acceleration due to gravity.

Given that the stomper stomps with an energy equal to 1/4 of applied by one of the jumpers.

Thus the total energy applied to the seesaw is given by,

`\begin{gathered} E_T=2M\text{gh}+(1)/(4)M\text{gh} \\ =(9)/(4)M\text{gh} \end{gathered}`

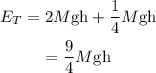
On substituting the known values,

`\begin{gathered} E_T=(9)/(4)*80*9.8*1 \\ =1764\text{ J} \end{gathered}`

a)

This total energy will be equal to the kinetic energy of Francine when she is shot off.

Thus,

`\begin{gathered} E_T=E_K=(1)/(2)mv^2 \\ \Rightarrow v=\sqrt[]{(2E_T)/(m)} \end{gathered}`

Where E_K is the kinetic energy of Francine when she is shot off and v is her velocity when she is shot off.

On substituting the known values,

`\begin{gathered} v=\sqrt[]{(2*1764)/(50)}_{} \\ =8.4\text{ m/s} \end{gathered}`

Thus Francine's velocity when she is shot off is 8.4 m/s

b)

The potential energy of Francine when she is at the maximum height is equal to the energy applied to the seesaw. Thus,

`\begin{gathered} E_T=E_P \\ =\text{mgH} \\ \Rightarrow H=(E_T)/(mg) \end{gathered}`

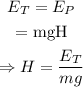
Where E_P is the potential energy of Francine and H is the height reached by Francine.

On substituting the known values,

`\begin{gathered} H=(1764)/(50*9.8) \\ =3.6\text{ m} \end{gathered}`

Thus the maximum height reached by Francine is 3.6 m