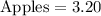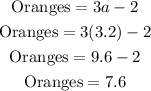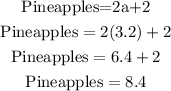Question

Isabella bought apples, oranges, and pineapples. The cost of the oranges is $2 less than thrice the cost of the apples and the cost of the pineapples is $2 more than twice of the cost of the apples. The total cost of the fruits is $18.95. Find the cost of each fruit. (Estimate to nearest tenths place).

Answer 1

Let the cost of each fruit be represented as follows;

`\begin{gathered} \text{Apples}=a \\ \text{Oranges}=b \\ \text{ Pineapples=c} \end{gathered}`

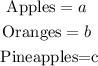
If the cost of the oranges is 2 dollars less than thrice the cost of the apples, then we would have;

`b=3a-2`

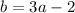
Also, if the cost of pineapples is 2 dollars more than twice the cost of the apples, then we would have;

`c=2a+2`

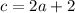
The total cost of the fruits is given as;

`a+b+c=18.95`

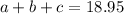
With the values of a, b and c now known;

`\begin{gathered} a+(3a-2)+(2a+2)=18.95 \\ a+3a-2+2a+2=18.95 \\ \text{Collect all like terms, and you'll have} \\ 6a=18.95+2-2 \\ 6a=18.95 \\ \text{Divide both sides by 6} \\ (6a)/(6)=(18.95)/(6) \\ a=3.158333\ldots \\ a\approx3.2 \end{gathered}`

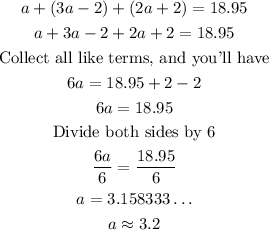
We can now substitute the value of a to determine the cost of each fruit as follows;

`\text{Apples}=3.20`
`\begin{gathered} \text{Oranges}=3a-2 \\ \text{Oranges}=3(3.2)-2 \\ \text{Oranges}=9.6-2 \\ \text{Oranges}=7.6 \end{gathered}`
`\begin{gathered} \text{ Pineapples=2a+2} \\ \text{ Pineapples}=2(3.2)+2 \\ \text{ Pineapples}=6.4+2 \\ \text{ Pineapples}=8.4 \end{gathered}`