Question

The length of a rectangle is 7 feet less than 5 times the width. If the perimeter is 94 feet, find the length and the width of the rectangle.

Answer 1

Let l be the length of the rectangle and w be its width.

Since the length is 7 feet less than 5 times the width, and the perimeter is 94 feet we can set the following system of equations:

`\begin{gathered} l=5w-7ft, \\ 2l+2w=94ft\text{.} \end{gathered}`

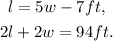
Substituting the first equation in the second one we get:

`2(5w-7ft)+2w=94ft\text{.}`

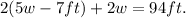
Applying the distributive property we get:

`10w-14ft+2w=94ft\text{.}`

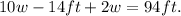
Adding like terms we get:

`12w-14ft=94ft\text{.}`

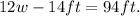
Adding 14ft to the above equation we get:

`\begin{gathered} 12w-14ft+14ft=94ft+14ft, \\ 12w=108ft\text{.} \end{gathered}`

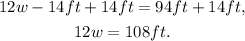
Dividing the above equation by 12 we get:

`\begin{gathered} (12w)/(12)=(108ft)/(12), \\ w=9ft\text{.} \end{gathered}`

Finally, substituting w=9ft in the first equation we get:

`\begin{gathered} l=5\cdot9ft-7ft=45ft-7ft \\ =38ft\text{.} \end{gathered}`

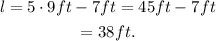
Answer: The length of the rectangle is 38ft and its width is 9ft.