Question

Find the equation of the parabola that has a vertex at (2,0) and a y-intercept of (0,12).Question 19 options:A) y = 3(x + 2)2B) y = (x – 2)2C) y = (x + 2)2D) y = 3(x – 2)2

Answer 1

Equation of a parabola is given by the equation

`y=a(x-h)^2+k`

Where (h, h) are the coordinates of the vertex.

From the question given, the vertex is (2, 0)

So, h = 2, k = 0.

The y-intercept is given as (0, 12).

So, this means that x = 0 and y = 12

Substituting the values for h, k, x and y into the equation we have

`\begin{gathered} y=a(x-h)^2+k \\ \\ 12=a(0-2)^2+0 \\ \\ 12=a*-2^2+0 \\ \\ 12=4a \\ \\ a=(12)/(4) \\ \\ a=3 \end{gathered}`

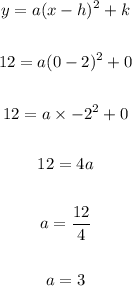
Now, let's substitute the value of a into the equation to get equation for the parabola.

This becomes

`\begin{gathered} y=a(x-h)^2+k \\ \\ y=3(x-2)^2+0 \\ \\ y=3(x-2)^2 \\ \\ \end{gathered}`