Question

Consider the following polynomial use polynomial division and the quadratic formula if necessary to identify the actual zeros

Answer 1

First, let's factor the given polynomial by grouping:

`\begin{gathered} g(x)=x^3-2x^2-2x+4\\ \\ g(x)=x^2(x-2)-2(x-2)\\ \\ g(x)=(x^2-2)(x-2) \end{gathered}`

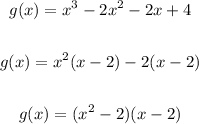
From the factor (x - 2), we can identify that x = 2 is one zero of the polynomial function.

Then, to find the other two zeros, let's equate the first factor to zero:

`\begin{gathered} x^2-2=0\\ \\ x^2=2\\ \\ x=\pm√(2)\\ \\ x_1=√(2)\\ \\ x_2=-√(2) \end{gathered}`

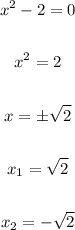
Therefore the zeros of this function are 2, √2 and -√2.