Question

I’m really struggling with this subject and need some help

Answer 1

Given:

A figure is given.

Required:

Find the value of x and y.

Step-by-step explanation:

Two lines are intersecting each other at a point so the opposite angles will be vertically opposite angles.

The vertically opposite angles are equal so

`\begin{gathered} (7x+15)\degree=(3x+85)\degree \\ 7x\degree+15\degree=3x\degree+85\degree \\ 7x\degree-3x\degree=85\degree-15\degree \\ 4x\degree=70\degree \\ x=17.5\degree \end{gathered}`

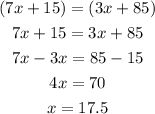
We know that the sum of linear angles is 18 degrees.

`2y\degree+(7x+15)\degree=180\degree`

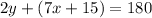
Substitute the value of x in the equation.

`\begin{gathered} 2y\degree+(7*17.5+15)=180\degree \\ 2y\degree+137.5\degree=180\degree \\ 2y\degree=180-137.5\degree \\ 2y\degree=42.5\degree \\ y=21.25\degree \end{gathered}`

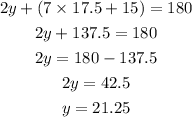
So the values are

`\begin{gathered} x=17.5\degree \\ y=21.25\degree \end{gathered}`

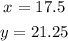
Final Answer:

Option b is the correct answer.