Question

In a survey of 1436 people 1039 people said they voted in a recent presidential election. Voting records show that 70% of eligible voters actually did vote. Given that 70% of eligible voters actually did vote.(a) find the probability that among 1438 randomly selected voters, at least 1039 actually did vote. (b) What do the results from part (a) suggest?

Answer 1

The variable in study is "The number of people that voted in the recent presidential election out of 1436 surveyed people"

Voting records show that 70% of the eligible voters did vote in the recent presidential election.

Considering that the variable follows the binomial criteria:

-The number of the trial is fixed, in this case, this number corresponds to the total number of people that answered the survey, so, n= 1436

- Each observation in the trial is independent, this means that none of the trials will have an effect on the probability of the next one, in this case, the answer of one person does not affect the probability of the answer of the next person.

- The probability of success is equal for all trials, in this case, the probability of success is the percentage of people that voted in the presidential election, so p=0.70

So you can say that the variable has a binomial distribution with parameters n=1436 and p=0.70

To calculate the probability P(X≥1039) you have to approximate the distribution of the sample proportion to normal using the central limit theorem.

The mean of the distribution will be equal to the population proportion μ=p and the variance is σ²= p(1-p)/n

`\hat{p}\approx N(p;(p(1-p))/(n))`

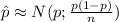
Using the approximation of the standard normal distribution derived from the distribution of the sample proportion:

`Z=\frac{\hat{p}\text{-p}}{\sqrt[]{(p(1-p))/(p)}}\approx N(0,1)`

First, express the given probability in terms of the sample proportion, by dividing the given value of x by the sample size:

`P(X\ge1039)\to P((X)/(n)\ge(1039)/(1436))=P(\hat{p}\ge0.7235)`

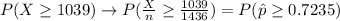
Next, calculate the Z-value that corresponds to the obtained sample proportion:

`\begin{gathered} Z=\frac{\hat{p}-p}{\sqrt[]{(p(1-p))/(n)}} \\ Z=\frac{0.7235-0.70}{\sqrt[]{(0.7(1-0.7))/(1436)}} \\ Z=\frac{0.0235}{\sqrt[]{(0.21)/(1436)}} \\ Z=1.943 \end{gathered}`

You can write the probability as follows:

`P(\hat{p}\ge0.7235)\to P(Z\ge1.943)`

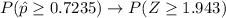
The normal distribution tables provide accumulative probabilities, so, to determine the probability of obtaining a value greater than or equal to 1.943, you have to apply the complement rule and subtract the probability of obtaining a value less than 1.943 to 1:

`P(Z\ge1.943)=1-P(Z<1.943)`

Using the standard normal distribution you can determine the probability of obtaining a value less than 1.943

`P(Z<1.943)=0.974`

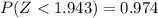
And use it to calculate the probability of obtaining a value greater than or equal to 1.943

`\begin{gathered} P(Z\ge1.943)=1-P(Z<1.943) \\ P(Z\ge1.943)=1-0.974 \\ P(Z\ge1.943)=0.026 \end{gathered}`

So the probability that 1039 or more people voted is 0.026.