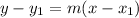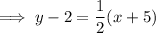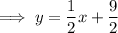Answer:
3)
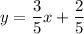
4) a)
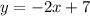
b)
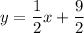
Explanation:
Exercise 3
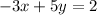
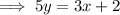
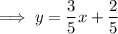
Exercise 4
a) If L2 is parallel to L1, it has the same slope (gradient) ⇒
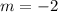
If L2 passes through point (3, 1):
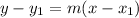
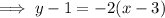
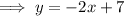
So L2 = L1
b) If L3 is perpendicular to L1, then the slope of L3 is the negative reciprocals of the slope of L1 ⇒
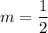
If L3 passes through point (-5, 2):