Solution:
Given the right triangle MXN as shown below:
To evaluate the measure of angle X to the nearest tenth,
step 1: Identify the sides of the triangle.
In the triangle MXN, using the angle X as the angle of focus,
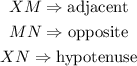
step 2: Evaluate the measure of angle X using trigonometric ratios.
From trigonometric ratios,
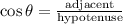
where
thus,
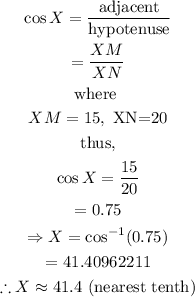
Hence, the measure of the angle X to the nearest tenth is 41.4 degrees.