Question

Need help finding the probability when there are 2 outcomes

Answer 1

First let's create the sample space of the experiment

let S denotes the sport car , T denote the pick up truck and R denotes the grandma ride.

Then the possible combinations will be

`\begin{gathered} (S,New),(S,Good),(S,Poor),(S,Fair), \\ (T,New),(T,Good),(T,Poor),(T,Fair), \\ (R,New),(R,Good),(R,Poor),(R,Fair), \end{gathered}`

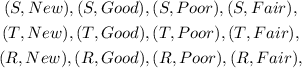
Now let E deontes the event of getting grandma ride and F denotes the event of getting new vehicle

Then

`n(E\cap F)=1`

So

`P(E\cap F)=(1)/(12)`

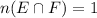
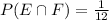
So the probabilty of getting a grandma ride and a vehicle in new condition is 1/12

Now let A denote the event of getting a sports car and B denote the event of getting a vehicle in fair condition so

`n(A\cup B)=6`

So

`P(A\cup B)=(6)/(12)`

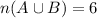
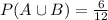
So the probabilty of getting a sports car or a vehicle in fair condition is 6/12