Question

Hint for exercises 3-4, you are given the sample mean and the sample standard deviation. Assume the population is normally distributed and use the T distribution, first find margin of error using= and then construct a 95% confidence interval for the population mean.In a random sample of eight people, the main commute time to work was 35.5 minutes and the standard deviation was 7.2 minutes. Construct a 95% confidence interval for the population mean. I have no idea where to begin with this I really need help if you could please explain and show me step by step so I can do the other exercises I have exactly like this one I would greatly appreciate it I have not done math in 25 years

Answer 1

(29.48, 41.52)

Explanation:

Given:

Mean (µ) = 35.5

Standard deviation (σ) = 7.2

Sample size (n) = 8

The confidence interval is 95%.

To determine the interval we have the following formula:

`\begin{gathered} CI=\mu\pm ME \\ \\ ME=z_(tc)\cdot(\sigma)/(√(n)) \\ \\ \text{ We replacing:} \\ \\ CI=\mu+z_(tc)\cdot(\sigma)/(√(n)) \end{gathered}`

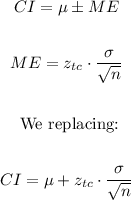
The value of critical z is given by the confidence interval since for 95% and for degrees of freedom 7 it is equal to 2.365

We substitute each value and calculate the interval, like this:

`\begin{gathered} CI_(upper)=35.5+2.365\cdot(7.2)/(√(8))=41.52 \\ \\ CI_(lower)=35.5-2.365\cdot(7.2)/(√(8))=29.48 \end{gathered}`

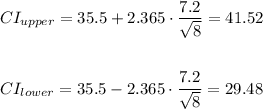
So the 95% confidence interval is (29.48, 41.52)