Question

Which ordered pair represent points on the graph of this exponential function?f(x) = 2^x+1

Answer 1

Given the exponential function:

`f(x)=2^x+1`

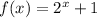
Let's find a list of ordered pairs which represent points on tyhe graph of this given function.

Let's evaluate f(x) for different values of x.

`\begin{gathered} when_{\text{ }}x=1\Longrightarrow f(1)=2^1+1=2+1=3 \\ \\ when_{\text{ }}x=2\Longrightarrow f(2)=2^2+1=4+1=5 \\ \\ when_{\text{ }}x=3\Longrightarrow f(3)=2^3+1=8+1=9 \end{gathered}`

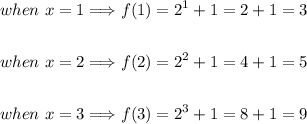
Thus, we have the soluttions:

When x = 1, f(x) = 3

When x = 2, f(x) = 5

When x = 3, f(x) = 9

Therefore, a possible list of ordered pairs for the function are:

(x, y) ==> (1, 3), (2, 5), (3, 9)

ANSWER:

• (1, 3)

,

• (2, 5)

,

• (3, 9)