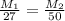Question

If M1 and M2 are the number of sexsimal and centesimal minute of any angle, prove that M1/27=M2/50Exercise 15(b)

Answer 1

Given the numbers of sexagesimal and centesimal minutes of any angle, you need to prove that:

`(M_1)/(27)=(M_2)/(50)`

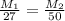
By definition, a Right Angle measures 90 degrees.

By definition, for Sexagesimal:

`1\text{\degree}=60\text{ }minutes`
`1\text{ }minute=60\text{ }seconds`

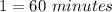
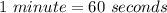
Then, in the sexagesimal form, a Right Angle is:

`90\cdot60\cdot60\text{ }seconds`

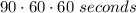
By definition, for Centesimal:

`90\text{\degree}=100\text{ }g`
`100\text{ }g=100\text{ }minutes`
`1\text{ }minute=100\text{ }seconds`

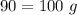
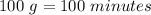
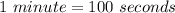
Therefore, a Right Angle is:

`100\cdot100\cdot100\text{ }seconds`

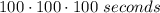
So you can set up this ratio:

`(M_1)/(M_2)=(90\cdot60)/(100\cdot100)`

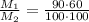
Simplifying, you get:

`(M_1)/(M_2)=(27)/(50)`

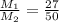
Hence, the answer is:

`(M_1)/(M_2)=(90\cdot60)/(100\cdot100)`
`(M_1)/(M_2)=(27)/(50)`

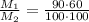
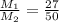
Therefore:

`(M_1)/(27)=(M_2)/(50)`