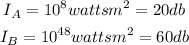Answer: We have to find the sound Intensity of sound B in Decibels, provided the sound Intensity of sound A is 20 Decibels. The Sound Intensity of B is 3 times the sound Intensity of sound A:
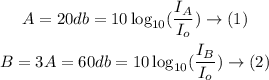
The threshold Intensity in equations (1) and (2) is as follows:
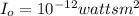
Solving the equation (1) gives:
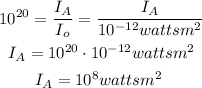
Same is true for the equation (2):
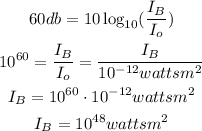
The answer, therefore, is as follows: