Question

The area of a rectangle is 14 m², and the length of the rectangle is 3 m less than twice the width. Find the dimensions of the rectangle.Length: Width :

Answer 1

Based on the question, here are the given data:

area of the rectangle = 14m²

length of the rectangle = 2w - 3 (3 meters less than twice the width)

The area of the rectangle is the product of length and width.

`\begin{gathered} A=l* w \\ 14^{}=(2w-3)* w \\ 14^{}=2w^2-3w \\ \text{Equate the equation into 0 by transferring 14m}^2\text{ to the opposite side.} \\ 2w^2-3w-14^{}=0 \\ \text{Factor out the equation above.} \\ (2w-7)(w+2)=0 \\ \text{Equate each factor into zero.} \\ 2w-7=0 \\ 2w=7 \\ w=(7)/(2)or3.5m \\ w+2=0 \\ w=-2m \end{gathered}`

Based on the solution above, there are two possible values of the width: 3.5 meters and -2 meters. Since there are no negative measurements, we'll not consider the -2m. Therefore, our width will be w = 7/2 or 3.5 meters.

From the value of the width, we can solve the length of the rectangle.

`\begin{gathered} \text{length}=2w-3 \\ \text{length}=2(3.5)-3 \\ \text{length}=4m \end{gathered}`

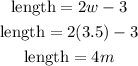
The length of the rectangle is 4 meters.