Question

This is a tough question for me. Can you solve it

Answer 1

`f(x)=(2x+3)(x-1)(x-4)`

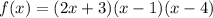
a) To find the root we have to set the function equal to zero

`\begin{gathered} (2x+3)(x-1)(x-4)=0 \\ \end{gathered}`
`\begin{gathered} (2x+3)=0 \\ x_1=-(3)/(2) \end{gathered}`
`\begin{gathered} x-1=0 \\ x_2=1 \end{gathered}`
`\begin{gathered} x-4=0 \\ x_3=4 \end{gathered}`

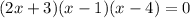
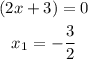
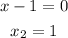
b) The intervals obtained when the x-intercepts are used to partition the number line are

`\begin{gathered} (-\infty,-(3)/(2))\to1 \\ (-(3)/(2),1)\to2 \\ (1,4)\to3 \\ (4,+\infty)\to4 \end{gathered}`

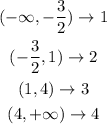
c) The table of signs

d) A sketch of the graph

What happens to the graph as x decreases?

• The graph tends to negative infinity

What happens to the graph as x increments?

• The graph tends to negative infinity

For which intervals is the graph above of x axis

`\begin{gathered} (-(3)/(2),1) \\ (4,+\infty) \end{gathered}`

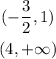
For which intervals is the graph below of x axis

`\begin{gathered} (-\infty,-(3)/(2)) \\ (1,4) \end{gathered}`

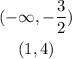
What is the leading term of the polynomial function?

To calculate the leading term we must expand the function

`(2x+3)(x-1)(x-4)=2x^3-7x^2-7x+12`

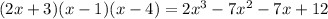
The leading term is the term with the highest exponent in this case x³

What is the leading coefficient of the polynomial function?

It is the number that accompanies the leading term in this case 2