Question

Object A is stationary while objects B and C are in motion.Forces from object A do 10 J of work on object B and –5 J ofwork on object C. Forces from the environment do 4 J of workon object B and 8 J of work on object C. Objects B and C donot interact. What are ∆Ktot and ∆Uint if (a) objects A, B, and Care defined as separate systems and (b) one system is defined toinclude objects A, B, and C and their interactions?

Answer 1

Given:

• Forces from object A:

Work on object B = 10 J

Work on object C = -5 J

• Forces from the environment:

Work on object B = 4 J

Work on object C = 8J

Given that the forces of objects B and C do not interact,

Let's find ∆K_tot and ∆U_nit.

When:

• (a). Objects A, B, and C are defined as separate systems.

Since object A is stationary, we have: ∆KA = 0 J

`\begin{gathered} \Delta K_B=10\text{ J + 4 J = 14 J} \\ \\ \Delta K_C=-5\text{ J + 8 J = 3 J} \\ \\ \Delta K_(tot)=0J+14J\text{ + 3 J = 17 J} \end{gathered}`

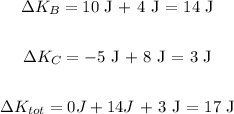
ii). Since all objects are defined as separate systems, all forces are external to the system.

Therefore, the change in U = 0

`\Delta K_(unit)=0\text{ }`

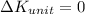
• (b). one system is defined to include objects A, B, and C and their interactions?

Here, if one system is defined to include the objects and their interactions, we have:

`\Delta K_(tot)=14J+3J\text{ = 17 J}`

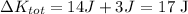
Also, for the change in U, we have:

`\Delta K_(unit)=-(10-5)=-10J+5J=-5J`

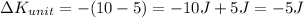
ANSWER:

(a). ∆Ktot = 17 J

∆Kunit = 0 J

(b). ∆Ktot = 17 J

∆Kunit = -5 J