We are given that a train brakes with a force of 1.64x10^6N. To determine its final speed after 31 seconds we need first to determine its acceleration. To do that we will use Newton's second law:
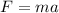
Where:
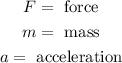
Now we solve for the acceleration by dividing both sides by "m":
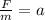
Now we substitute the given values:
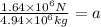
Solving the operations we get:
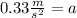
Now we use the following equation of motion to determine the final speed:
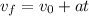
Where:
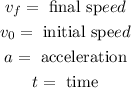
Now we substitute the values:
![v_f=56.1\frac{\operatorname{km}}{h}-(0.33(m)/(s^2))(31s)]()
We need to convert the km/h into m/s. To do that we will use the following conversion factors:
![\begin{gathered} 1\operatorname{km}=1000m \\ 1h=3600s \end{gathered}]()
Now we multiply the initial velocity by the conversion factors:
![56.1\frac{\operatorname{km}}{h}*\frac{1000m}{1\operatorname{km}}*(1h)/(3600s)=15.58(m)/(s)]()
Now we substitute the value:

Solving the operations we get:
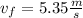
Therefore, the final velocity is 5.35 meters per second.
Now we are asked to determine the distance traveled by the train. To do that we will use the following equation of motion:
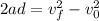
Where:
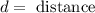
Now we solve for the distance by dividing both sides by "2d":
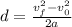
Now we substitute the values:
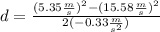
Solving the operations:
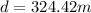
Therefore, the distance is 324.42 meters.