Question

Hi! I don’t know how to do this, can somebody help?

Answer 1

Given:

The function are,

`g(x)=6x^2-5`

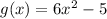
and

`f(x)=x^2`

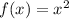
Step-by-step explanation:

The function g(x) i a quadratic function and quadratic function is defined for all values of x. So domain of function f(x) is all real numbers.

The x-coordinate vertex of parabola ax^2 + bx + c = 0 is,

`-(b)/(2a)`

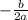
Fo the given quadratic equation a = 6, b = 0 and c = -5. So x-coordinate of vertex is,

`-(0)/(2\cdot6)=0`

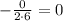
Determine the y-coordinate of vertex.

`\begin{gathered} g(0)=6\cdot(0)^2-5 \\ =-5 \end{gathered}`

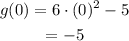
So minimum value of function is -5.

So range of function g(x) is,

`\lbrack-5,\infty)`

Domain and range in interval notation:

Domain:

`(-\infty,\infty)`

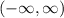
Range:

`\lbrack-5,\infty)`

Domain and range in set notation:

Domain:

`\mleft\lbrace x|x\in\mathfrak{\Re }\mright\rbrace`

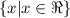
Range:

`\mleft\lbrace y|y\ge-5\mright\rbrace`

Domain and range in inequality notation:

Domain:

`-\inftyRange:[tex]-5\leq y<\infty`

On compare the function g(x) with f(x), it can be observed that value of factor a is 6, which means function stretch vertically by a factor of 6.

The value of k is -5, means function translated down by 5 units.

Answer:

When compared to f(x), g(x) is stretched verticaly by a factor of 6, and translated down 5 units.