Question

Determine whether the following system of equations is consistent or inconsistent and dependent or independent

Answer 1

Given the system of equations:

`\begin{gathered} y=(1)/(3)x+4 \\ \\ y=-3x+2 \end{gathered}`

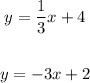
Ley's determine if the system is inconsistent or consistent and dependent or independent.

Let's first solve the system of equations.

Eliminate the equivalent sides and combine the equations.

We have:

`\begin{gathered} (1)/(3)x+4=-3x+2 \\ \\ (x)/(3)+3x=2-4 \end{gathered}`

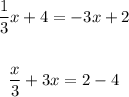
Solving further:

`\begin{gathered} (x+9x)/(3)=-2 \\ \\ (10x)/(3)=-2 \\ \\ Multiply\text{ both sides by 3:} \\ (10x)/(3)*3=-2*3 \\ \\ 10x=-6 \\ \\ Divide\text{ both sides by 10:} \\ (10x)/(10)=-(6)/(10) \\ \\ x=-(3)/(5) \end{gathered}`

Now, plug in -3/5 for x in any of the equations:

`\begin{gathered} y=(1)/(3)x+4 \\ \\ y=(1)/(3)*(-(3)/(5))+4 \\ \\ y=-(1)/(5)+4 \\ \\ y=(-1+20)/(5) \\ \\ y=(19)/(5) \end{gathered}`

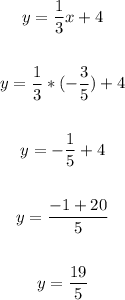
Therefore, we have the solutions:

`(x,y)==>(-(3)/(5),(19)/(5))`

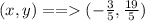
The system is consistent and independent since it has a definite solution.

The system has just one solution, so we can say it is consistent and independent.

ANSWER:

Consistent and independent.