Solution
- The formula for finding the Perimeter of a square is:
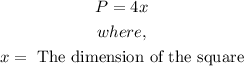
- The perimeter of a rectangle is:
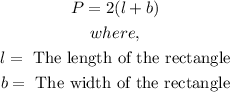
- The perimeter of the square garden will be:
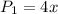
- The Perimeter of the whole rectangular garden is:
![\begin{gathered} P_2=2([26+x]+x) \\ where, \\ l=26+x \\ b=x \\ \\ \therefore P_2=2(26+2x) \\ \\ P_2=52+4x \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/woj8jx6r4x5x3q1aptb1zrwhqsd3f8myyx.png)
- We are also told that if the gardener is to fence the whole rectangular garden, he'd use twice as much fencing.
- This implies that
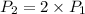
- Substituting the expressions for P2 and P1 into the above expression, we can find the value of x and subsequently, the total amount of fencing he will need.
- This is done below:

- Now that we have the value of x, we can proceed to find the total amount of fencing needed.
- This is
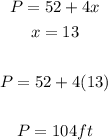
Final Answer
The total fencing needed is 104 ft