We have a sample that is: 6, 4, 3, 5, 4, 2, 4, 5, 4, 6, 1, 4, 5, 2.
a) We have to construct a frequency distribution table.
We have to include the proportion (relative frequency) and percentage.
We can complete this table as:
The frequency is the count of the appearance of each category (in this case, each score).
The relative frequency or proportion is equal to the frequency divided by the sample size (n = 14).
b) To know what percent is 3 or lower, we can add the percentage for the three first three rows:
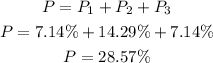
c) The percent that is 4 or higher will be the complement of the previous calculation, as if it is not 3 or lower, it will be 4 or higher.
Then, we can calculate it as:
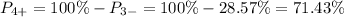
d) We haveto compute the mean, the median, the variance and the standard deviation.
We can start with the mean as:
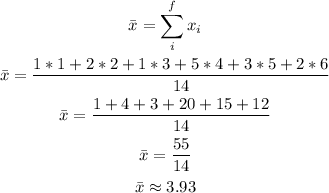
The median will be the average between the 7th and 8th place for the sample when sorted from least to greatest.
We then sort the sample as: