Answer: x= -1, x = 2 and x = 3
In order to graph out the equation given, we need to create a table of values that will guide us.
This table of values shall contain values of x and corresponding values of y.
For the values of x, we shall use integers ranging from -2 to +4.
While for the values of y, we shall plug in this chosen x-coordinates into the equation given.

Now, to get the y-values and hence create the table of values which will be used to plot the graph:
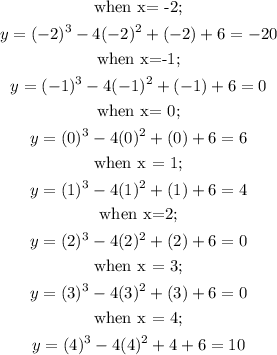
Thus, the coordinates of the equation are:
(x, y):
(-2, -20), (-1, 0), (0, 1), (1, 4), (2, 0), (3, 0), (4, 10)
We can therefore create a table of values for the calculated coordinates of the equation
Now with this table of values, you can plot the graph. The picture of the plotted graph is shown below:
The solutions to the equation are where the graph crosses the x-axis.
By reading the graph above, the solutions are:
x= -1, x = 2 and x = 3
Therefore, the final answer is: x= -1, x = 2 and x = 3