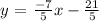Question

Write the equation of the line that passes through the points (-8,7) and (2, -7).Put your answer in fully simplified point-slope form, unless it is a vertical orhorizontal line.

Answer 1

Answer: y = -7/5x -21/5

Explanations:

GIVEN POINTS

• ( x1;y1 ) = ( -8;7)

,

• (x2;y2 ) = (2;-7)

(i) Calculate the Slope -substitude given point into the slope formula below:

`\begin{gathered} Slope\text{ \lparen m\rparen = }(y_2-y_1)/(x_2-x_1) \\ \text{ = }\frac{-7\text{ -7}}{2-(-8)} \\ \text{ =}(-14)/(10) \\ \text{ =-}(7)/(5) \\ \text{ } \end{gathered}`

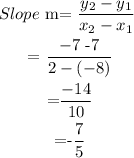
Therefore , the slope = -7/5

Our equation will follow the standard equation of a straight line :

`\begin{gathered} y\text{ = mx +c } \\ where\text{ m = -7/5 and c is the y intercept } \end{gathered}`

(ii) Calculate the y - intercept

• Now, our equation looks like this ,: y = -7/5x +c

,

• Subtitute any of the given point and solve for point c , lets choose point (, 2;-7),

`\begin{gathered} y\text{ = -}(7)/(5)\text{ + c ....at point \lparen 2;-7\rparen } \\ -7\text{ = -}(7)/(5)(2)\text{ +c } \\ -7\text{ = }(-14)/(5)\text{ +c} \\ -7\text{ +}(14)/(5)\text{ = C } \\ \therefore C\text{ = -21/5} \end{gathered}`

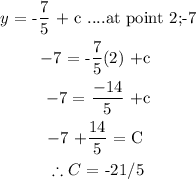
This means that the C value = -21/5

Our final equation of the line that passes through the given points will be :

`y\text{ = }(-7)/(5)x-(21)/(5)`