Given a logarithmic function in the form
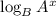
It is simplified according to the power law of logarithm as
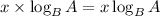
When it is in the form
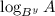
It is simplified according to the Base power law of logarithm as

Thus,
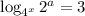
...is simplified as
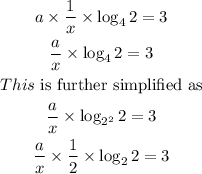
But

Hence, we have
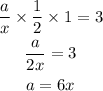
Hence the solution in terms of x is given as a=6x