Question

Given a homogeneous system of linear equations Ax = 0, if the determinant of A isO(zero), Ax = 0 has infinitely many solutions.True or False

Answer 1

Given:

A homogeneous system of linear equations Ax= 0 is given.

If the determinant of A is 0 then Ax = 0 has infinitely many solutions.

If the determinant is zero that means the matrix A is not invertible.

That implies there exists a non zero x such that Ax=0 that is,

`\Rightarrow x(\\e0)\in R^n\text{ such that Ax=0}`

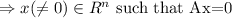
Then by linearity of A, every scalar multiple of x is mapped to zero by A.

Therefore, the system yields an infinite number of solutions.

Therefore, the statement is a true statement.