Question

A rectangular box with height 2 centimeters has a volume of 50cubic centimeters. The length of the box is 5 more than twicethe width. Find the dimensions of the box. This works with Quadratic Modeling. How do I solve this??

Answer 1

hello

to solve the question presented here, we need to apply the formula of area and perimeter of a rectangle

height = 2 cm

volume = 50cm^3

length = 5 + 2x

width = x

volume = length * width * height

we can simply plug in the variables and get an equation

`\begin{gathered} volume=length* wi\differentialD tth* height \\ 50=(5+2x)* x*2 \\ 50=2x(5+2x) \\ 50=10x+4x^2 \\ 4x^2+10x-50=0 \\ 2x^2+5x-25=0 \end{gathered}`

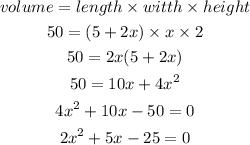
since we have our quadratic equation, we can proceed to solve through using any of the methods

during the process of this session, i'll use formula method

`\begin{gathered} 2x^2+5x-25=0 \\ a=2 \\ b=5 \\ c=-25 \\ x=-b\pm(√(b^2-4ac))/(2a) \\ x=-5\pm(√(5^2-4\cdot2\cdot(-25)))/(2\cdot2) \\ x=-5\pm(√(25--200))/(4) \\ x=-5\pm(√(25+200))/(4) \\ x=-5\pm(15)/(4) \\ x=(-5+15)/(4)\text{ or x = }(-5-15)/(4) \\ x=(10)/(4)\text{ or x = -5} \\ x=2.5\text{ or -5} \end{gathered}`

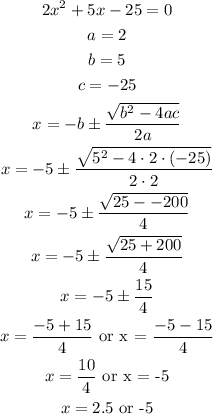
but dimension can't be negative

x = 2.5

width = 2.5cm

length = 5+ 2*2.5 = 10cm

height = 2cm