Question

random variables, probability distributions and expected value A lottery ticket can be purchased for $5. There are multiple prize options, shown along with the number of prizes, in the table below. What is the expected win (or loss) for this lottery ticket? Round your answer to the nearest cent. Do not round until your final answer.

Answer 1

To the table I'll add the probability of winning each of these prices. The total number of prizes is the sum of all the numbers on the second column, so it's 100,000

price number of prizes Probability fo winning

$50000 5 5/100,000

$5000 15 15/100,000

$50 100 100/100,000

$5 5000 5,000/100,000

lose 94880 94,880/100,000

To find the expected win (or loss) of a lottery ticket we have to multiply the probabilities of winning each price by their profits (the amount of the prize minus the price of the ticket)

`P(50000)(50000-5)+P(5000)(5000-5)+P(50)(50-5)+P(5)(5-5)+P(lose)(-5)`
`(5)/(100,000)\cdot49,995+(15)/(100,000)\cdot4,995+(100)/(100,000)\cdot45+0-(94,880)/(100,000)\cdot5`
`2.49975+0.74925+0.045+0-4.744=-1.45`

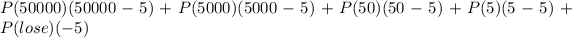
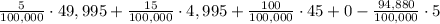
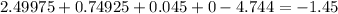
The expected win (or loss) for this lottery ticket is -1.45 (it's actually a loss)