Question

Find f '(x) of f(x) = 3/2x+4

Answer 1

Given:

`f(x)=3\sqrt[]{2x+4}`

The objective is to find inverse of the function.

Consider the given function as,

`y=3\sqrt[]{2x+4}`

The inverse of the function can be calculated by replacing the varibales x and y of the function.

Then, the function will be,

`x=3\sqrt[]{2y+4}`

Now, solve for y.

`\begin{gathered} (x)/(3)=\sqrt[]{2y+4} \\ 2y+4=((x)/(3))^2 \\ 2y+4=(x^2)/(3^2)^{} \\ 2y=(x^2)/(9)^{}-4 \\ y=(1)/(2)((x^2)/(9)^{}-4) \\ y=(x^2)/(18)^{}-(4)/(2) \\ y=(x^2)/(18)^{}-2 \end{gathered}`

Thus, the inverse function is,

`f^(-1)(x)=(x^2)/(18)^{}-2`

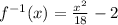
Hence, the required inverse of the function is obtained.