In the figure below, ZABC = ZDEC and ZGFE - ZDCE. Point C is the point of intersectionbetween AG and BD, while point E is the point of intersection between AG and DFProve ABC - …

Question

asked Mar 26, 2023 104k views

1 Answer

Nickcan · Answer 1 · 2023-03-31T05:43:53+0000

Given that

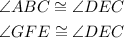
$\begin{gathered} \angle ABC\cong\angle DEC \\ \angle GFE\cong\angle DEC \end{gathered}$

C is the point of intersection between AG and BD while E is the point of intersection between AG and DF

To prove the triangle ABC is similar to the triangle GEF

From the given figure, it is seen that

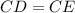
Therefore,

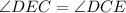
$\angle DEC=\angle DCE$

Since

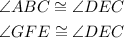
$\begin{gathered} \angle ABC\cong\angle DEC \\ \angle GFE\cong\angle DEC \end{gathered}$

Then,

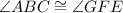
$\angle ABC\cong\angle GFE$

In the triangle ABC and the triangle GFE, two angles are congruent.

Therefore,

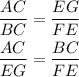
$\begin{gathered} (AC)/(BC)=(EG)/(FE) \\ (AC)/(EG)=(BC)/(FE) \end{gathered}$

Similarly,

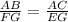
Thus,

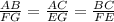
Hence, the triangle ABC is similar to the triangle GEF