Question

12. Jason wants to walk the shortest distance to getfrom the parking lot to the beach.RefreshmentStand40 mBeach30 mParkingLota.How far is the spot on the beach from theparking lot?How far will his place on the beach be fromthe refreshment stand?b.

Answer 1

In order to find the distance between the parking lot and the beach, we can use sine and cosine relations of the angles shown below:

Knowing that these angles are congruent and using the sine relation of the blue angle and the cosine relation of the green angle, we have:

`\begin{gathered} \sin (\text{blue)}=(h)/(30) \\ \cos (\text{green)}=(h)/(40) \end{gathered}`

Now, since the angles are the same, we can use the property:

`\begin{gathered} \sin ^2a+\cos ^2a=1 \\ ((h)/(30))^2+((h)/(40))^2=1 \\ (h^2)/(900)+(h^2)/(1600)=1 \\ (16h^2+9h^2)/(14400)=(14400)/(14400) \\ 25h^2=14400 \\ 5h=120 \\ h=24 \end{gathered}`

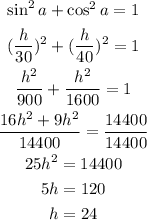
So the distance wanted is 24 meters.

b) Now, let's find the distance from the beach to the refreshment stand using the Pythagorean theorem in the upper right triangle:

`\begin{gathered} h^2=a^2+b^2 \\ 40^2=24^2+x^2 \\ 1600=576+x^2 \\ x^2=1024 \\ x=32 \end{gathered}`

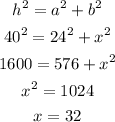
So the distance wanted is 32 meters.