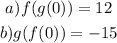The notation f(g(x)) means that you have to calculate the composition of the functions, that is, calculate f(x) when x=g(x)
Item a f(g(0))
You have to calculate f(x) when x=g(0)
The first step is to calculate g(0) → i.e. g(x) for x=0
You have to replace the function with x=0 and calculate its value:
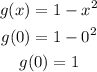
Now that we have determine the value of g(0), you have to replace it in f(x)
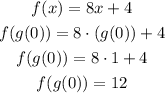
Item b g(f(0))
In this item you have to calculate g(x) when x=f(0)
The first step is to calculate f(x) for x=0
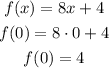
Once you calculated the value of f(0), you have to replace its value in the function g(x)
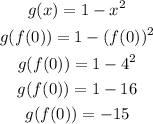
So the results are