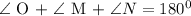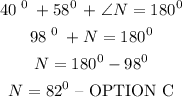SOLUTION:
Step 1 :
In this question, we are given measures of some angles in the diagram.
From the diagram, we can see that :
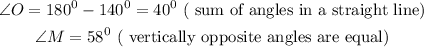
Then, we are meant to find the value of angle N.
Step 2 :
Recall that the sum of angles in a triangle = 180 degrees.
Then we have that: