The number on the dice from 1 to 6
Since we have 2 dice then the total out com will be 6 x 6 = 36
Let us find all outcomes

Now we need to find the probability of an even number
The even numbers are the numbers that end by 0, 2, 4, 6, or 8
Then we will find all the outcomes that given an even number
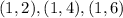
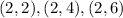
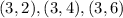
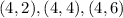
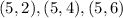
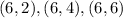
Then there are 18 even numbers, then the probability of an even number is
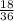
For a number greater than 7, The outcomes are
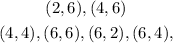
There are 6 numbers greater than 7
The probability of a number greater than 7 is
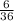
For or we will add the 2 probabilities
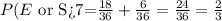
The answer is 24/36 or 2/3