Question

Is the sequence 0.5, 2, 8, 32, 128 an arithmetic or geometric sequence and why?

Answer 1

For an arithmetic sequence, there is a common difference between the adjacent numbers. An arithmetic sequence starting with the number can be given as,

a, a+d, a+d+d+a+d+d+d,...

a,a+d, a+2d, a+3d....

Here, d is the common difference

Consider the sequence, 0.5, 2, 8, 32, 128 .Fiirst find the difference between adjacent numbers.

`\begin{gathered} 2-0.5=1.5 \\ 8-2=4 \end{gathered}`

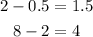
So, there is no common difference between adjacent numbers. Therefore, the sequence 0.5, 2, 8, 32, 128 is not an arithmetic sequence.

A geometric sequence is given by,

`a,ar,ar^2,ar^3,\ldots.`

Here, each term after the first is multiplied by a common factor r.

Now, divide each term by the previous term in the sequence 0.5, 2, 8, 32, 128 and find if there is any common factor.

`\begin{gathered} (2)/(0.5)=4 \\ (8)/(2)=4 \\ (32)/(8)=4 \\ (128)/(32)=4 \end{gathered}`

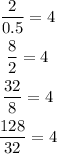
Since each term in the sequence 0.5, 2, 8, 32, 128 except the first term is obtained by multiplying the previous term by a factor 4, the sequence is a geometric sequence.