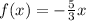Question

Can you help me to do this please?Finding the inverse of each funtion

Answer 1

To find the inverse of the function.

Given function is,

`g(x)=-(3)/(5)x`

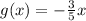
we know that,

The inverse function returns the original value for which a function gave the output.

Consider the function,

`y=-(3)/(5)x`

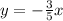
replace x by y and y by x, we get,

`x=-(3)/(5)y`

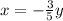
Solve for y we get,

`-3y=5x`
`y=-(5)/(3)x`

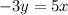
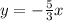
The inverse function f(x) is,

`f(x)=-(5)/(3)x`

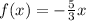
The inverse function is,

`f(x)=-(5)/(3)x`