Given:
The first term is 1.5.
The second term is 2.25.
The third term is 3.375.
And so on.
To determine:
The graph represents an arithmetic sequence or not.
Step-by-step explanation:
Let us check the common difference.
The first difference is,
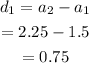
The second difference is,
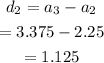
Since,
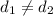
Therefore, it does not represent an arithmetic sequence.
Final answer:
The graph shown does not represent an arithmetic sequence.